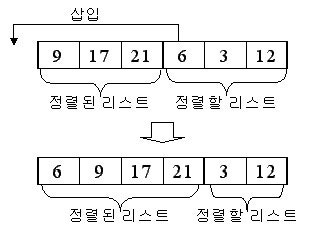
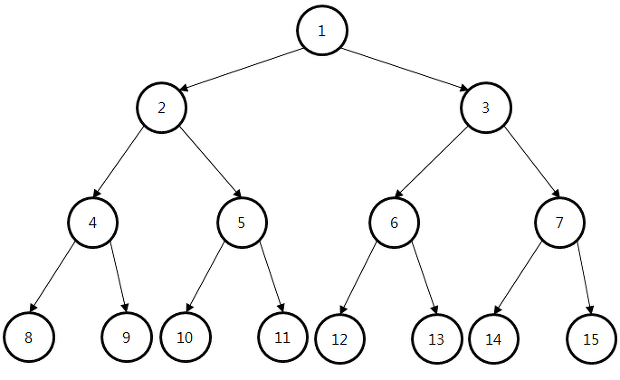
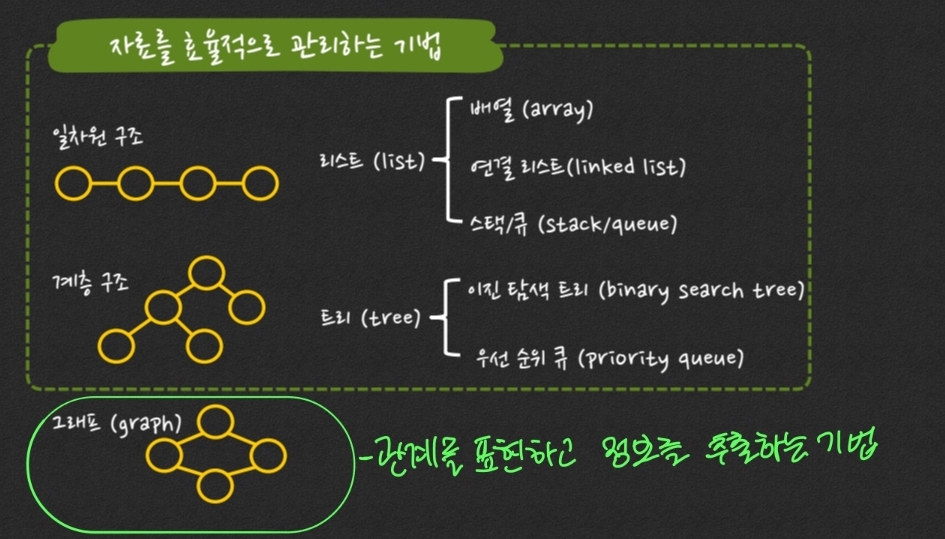
성능

성능이란 무엇인가?

정답을 빠른 시간 내에 출력: 요구하는 자원이 최소 -> 성능, 효율이 좋다

performance (efficiency) = 결과/비용

• 성능 또는 효율: 일을 잘 한다 + 소요된 시간 (자원)이 적다

성능의 세가지 측면

1. 최선의 경우 : 빠르면 1초 내에 검색
2. 평균의 경우: 평균 10초 내에 검색
3. 최악의 경우: 아무리 늦어도 1분 이내에 검색

-> 최선, 평균의 경우는 과장광고.. 최악의 경우로 말해야 사용자의 만족도에 도움이 됨

최악의 경우를 보장하는 것

자원의 두 가지 측면: 공간과 시간

공간 복잡도 space-complexity

• 공간에 관련된 성능
• 특정 프로그램을 수행하는 데 요구되는 메모리
• memory

시간 복잡도 time-complexity

• 시간에 관련된 성능
• 특정 프로그램을 수행하는 데 요구되는 시간
• cpu

시간이 공간보다 소중한 자원이다.

cpu가 더 비쌈

예) n 개의정수를입력받아서합을구하는프로그램

1. 정수를 하나씩 읽어서 합을 구함

int i, x, sum;
    for ( i = 0, sum = 0; i < n; i++ ) {
        cin >> x;
        sum += x;
    }
cout << sum;

- 공간 복잡도 O(1)

n의 크기에 관계없이 일정한 공간만을 요구함

변수 3개의 공간만 쓰면 됨, n번 실행함

- 시간 복잡도 O(n)

n의 크기에 비례해서 시간이 걸림

for문 n번 루프

2. 정수를 하나씩 읽어서 저장한 후에 합을 구함

int i, *x, sum;
x = new int[n];
for ( i = 0; i < n; i++ )
    cin >> x[i];
for ( i = 0, sum = 0; i < n; i++ )
    sum += x[i];
cout << sum;

int i, *x, sum;
x = new int[n];                          // O(1) - 메모리 할당 (크기는 n이지만 상수 시간에 이루어짐)
for ( i = 0; i < n; i++ ) cin >> x[i];  // O(n) - 입력을 n번 받음
for ( i = 0, sum = 0; i < n; i++ )      // O(n) - n개의 요소를 더함
    sum += x[i];
cout << sum;                            // O(1) - 출력 한 번

- 공간 복잡도 O(n)

n의 크기에 비례해서 공간을 요구함

n개의 저장공간 요구

- 시간 복잡도 O(n)

n의 크기에 비례해서 시간이 걸림

for문 n번 루프 두번

O(n)+O(n)=O(n)

점근적 분석법

(asymptotic complexity)

성능은 입력의 크기에 따라 결정됨

n:입력의 크기

시간복잡도를 n의 함수로 표현 -> f(n)

성능 그래프: (n,f(n))

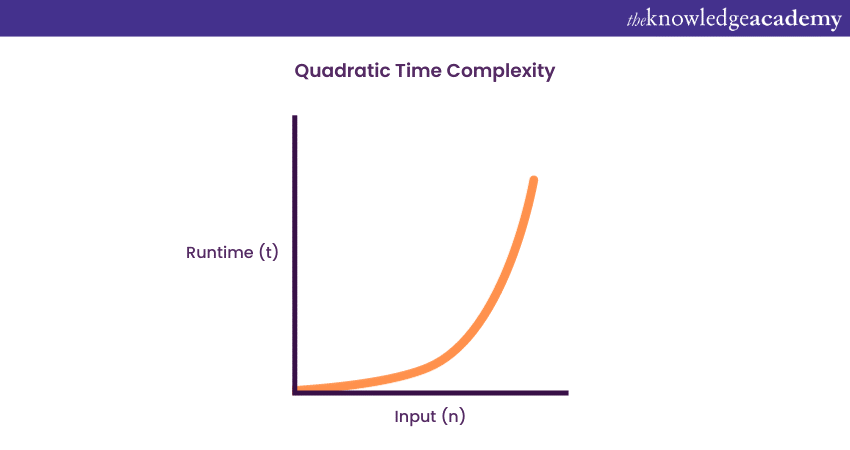
1) 입력이 증가하면 시간도 증가 (일반적)

2) 입력이 증가해도 시간은 일정 (이상적)

3) 입력이 증가하면 시간이 감소 (있을수없음)

시간 복잡도는 매우 큰 입력 (reasonably large length of input) 에 대해서 측정함

n이 매우 큰 경우에 대해서만 의미 잇는 성능이 측정됨

g(n)을 이용한 f(n)의 성능 표현

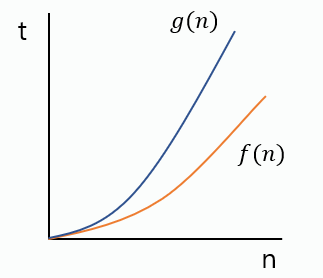
동일한 크기의 입력을 처리할 때, g(n)은 f(n)보다 더 많은 시간을 요구함

= g(n)은 f(n)보다 성능이 나쁨

= g(n)은 f(n)의 최악의 경우

f(n)의 상한은 g(n)

f(n) ≤ g(n)

• g(n)은 f(n)의 성능을 나타내는 척도로 사용됨
• 많이 사용되는 표준적인 함수 (1, n, log n, n², n log n, nⁿ) 이용

요약

(1) 최악의 경우의 성능 -> 보장
(2) 공간 복잡도보다 시간 복잡도가 더 중요
(3) (입력의 크기, 계산 시간) -> (n, f(n))
(4) 점근적 분석법 -> 매우 큰 입력을 가정
(5) 표준 함수를 사용 ->1, n, n², 2n, log n
(6) Big-O표기법: (1)+(2)+(3)+(4)+(5)

big-O 표기법

빅오 표기법의 정의

f(n) is O( g(n)) as n->∞

1. f(n) ≤ g(n)
2. f(n) ≤ g(n) for  n₀ <n      -> 항상 n₀보다 큰 n에 대해서만 요구하겠다
3. f(n) ≤ M g(n) for  n₀ <n  -> 동일한 비율로 증가하는 함수를 허용하기 위해서 상수 M을 인정함

3번 : g(n)이 5n이든 10n이든 f(n)=n에 비례함

성질 1

어떤 n > n₀ 에 대해서 g₁(n) < g₂(n) 이라면 f(n) = O( g₁(n) )은 f(n) = O( g₂(n) )을 의미한다.

예) f(n) = O(n)라면 f(n) = O(n²)이다.

증명)

f(n) ≤ M g₁(n) --- (정의 1)

g₁(n) < g₂(n)

-> f(n) ≤ M g₁(n) ≤ M g₂(n)

-> f(n) ≤ M g₂(n)

성질 2

어떤 상수 k에 대해서  f(n) = O( k g(n) )이라면, f(n) = O( g(n) )이다.

예) f(n) = O( 5n² )라면 f(n) = O( n² )이다.

성질 3

f(n) = O( g₁(n)+ g₂(n) ) 이고 어떤 n > n₀ 에 대해서  g₁(n) < g₂(n) 이라면 f(n) = O( g₂(n) )이다.

예) f(n) = O( n²+n )이라면 f(n) = O( n² )이다.

1-1

문제 1.

우리가 사용하는 다양한 앱에서는 (　　　　)를 효율적으로 관리하는 기법이 구현되어 있다.
답: 자료

문제 2.

기차표 예매와 수강 신청 등을 관리하는 시스템에서는 자료와 함께 (　　　　)를 관리한다.
답: 순서

1-2

문제 1.

다음 문장의 빈칸에 들어갈 말은?

컴퓨터에 저장할 수 있도록 프로그래밍 언어에서 미리 정의된 값들의 집합을 (　　　　)이라고 한다.

답: 자료형

문제 2.

16 bit로 세상의 모든 문자를 표현할 수 있는 체계를 (　　　　)라고 한다.

1. EBCDIC 코드
2. Uni 코드
3. BCD 코드
4. ASCII 코드

답: 2. Unicode

해설:

• ASCII: 7bit (128자만 표현 가능)
• EBCDIC: IBM의 8bit 문자 인코딩
• BCD: Binary-Coded Decimal, 숫자 표현 방식
• Unicode: 다양한 언어의 문자를 16bit 이상으로 표현 가능한 체계

문제 3.

정수형 표현에서 1의 보수와 2의 보수는 (　　　　)을(를) 표현하기 위한 방법이다.
답: 음수

1-3

문제 1.

다음 문장의 참과 거짓을 판정하시오.

정렬된 리스트에서는 자료의 위치를 예측할 수 있기 때문에 효율적인 검색이 가능하다.

답: 참

문제 2.

자료를 만난 순서에 따라서 저장하는 구조를 다음 중에서 선택하시오.

1. 큐
2. 리스트
3. 스택
4. 배열

답: 1

문제 3.

족보와 같은 계층 구조를 효율적으로 표현하는 구조를 (　　　　)(이)라고 한다.
답: 트리

2-1

문제 1.

특정한 프로그램을 수행하는 데 요구되는 메모리의 크기를 (　　　　)(이)라고 한다.
답: 공간 복잡도

문제 2.

점근적 분석법에서 성능은 (　　　　)에 따라서 결정된다.
답: 입력의 크기

문제 3.

다음 네 가지 표현 중에서 그 의미가 다른 것은 무엇인가?

1. f(n)의 하한은 g(n)임
2. 최악의 경우에도 f(n)은 g(n)보다 좋음
3. g(n)은 f(n)보다 성능이 나쁨
4. f(n) ≤ g(n)

답: 1

해설:

1. "하한"은 보통 Ω(𝑔(𝑛))를 의미 → f(n)이 최소한 g(n)만큼의 성능을 요구함 → 나머지 선택지들과 방향이 다름
2. ~ 4. 모두 f(n)이 g(n)보다 작거나 같다는 식의 의미를 갖고 있어, 상대적으로 f(n)의 성능이 더 좋다는 쪽에 가까움

2-2

문제 1.

f(n) = O(5n log n)이라면, f(n) = O(g(n))이다에서 g(n)에 올 수 없는 함수는?

1. n log n
2. n
3. n³
4. n²

답: 2

문제 2.

If g(n) ≥ M f(n) for n > n₀, then g(n) = (　　　　). 에서 (　　　　)에 들어갈 식은?

답: Ω(f(n))

해설:
g(n) ≥ M·f(n) for n > n₀ 은 f(n)에 대한 하한(bound from below)을 의미

문제 3.

f(n) = O(n² + n)이라면, f(n) = O(g(n))이다. g(n)에 올 수 없는 함수는?

1. n³
2. n
3. n²
4. n⁴

답: 2

해설:
f(n) = O(n² + n) 은 O(n²)와 같다고 볼 수 있음
(n²), (n³), (n⁴) → f(n)의 상한이 될 수 있음
하지만 n은 f(n)보다 작기 때문에 상한으로는 올 수 없음

2-3

문제 1.

n 명인 반의 학생들이 모두 키 순으로 앉아있다. 여기에 새로운 학생 한 명이 전학을 왔다. 이 학생을 그냥 맨 앞에 앉도록 할 때, 걸리는 시간 복잡도는 무엇인가?

1. O(n)
2. O(n log n)
3. O(1)
4. O(log n)

답: 1

문제 2.

int func (int n) {
  for (k = 1; k < n; k = k * 10)
    printf("hello");
}

다음 함수의 시간 복잡도를 n의 함수로 나타내시오.

1. O(log n)
2. O(n log n)
3. O(n²)
4. O(n)

답: 1

문제 3.

다음 중 시간 복잡도가 가장 큰 함수는 무엇인가?

1. O(nⁿ)
2. O(n¹⁰⁰)
3. O(n!)
4. O(2ⁿ)

답: 1

해설:
(시간 복잡도 크기 순으로 정리):
𝑂(𝑛¹⁰⁰) → 다항식 (Polynomial)
𝑂(2ⁿ) → 지수 함수 (Exponential)
𝑂(𝑛!) → 팩토리얼 (Factorial)
𝑂(𝑛ⁿ) → 지수보다도 빠르게 커지는 초지수 함수

3-1

문제 1.

리스트의 가장 중요한 성질은 모든 원소들이 (　　　　)에 1:1로 대응된다는 점이다.
답: 인덱스

문제 2.

연결 리스트는 리스트를 (　　　　)에 기반하여 구현한 자료구조이다.
답: 포인터

문제 3.

“정렬되지 않은 리스트에서 원소를 추가하는 연산은 정렬된 리스트에서 원소를 추가하는 연산보다 더 좋은 시간 복잡도를 보인다”는 문장의 참과 거짓을 쓰시오.(참 또는 거짓을 쓸 것)
답: 참

3-2

문제 1.

n개의 원소를 가진 배열에 대한 이진 검색의 시간 복잡도는 (　　　　)이다.

오답: O(n) -> 이건 선형검색

정답: O(log n)

해설:

매번 검색 범위를 절반으로 줄임

문제 2.

n개의 원소를 가진 배열에 대한 선형 검색은 최선의 경우에는 [ ]의 시간이 걸리지만 최악의 경우에는 [ ]의 시간이 걸린다. 빈칸을 Big-O 표기법으로 표현한 쌍 중에서 맞는 것은?

1. O(1), O(n)
2. O(log n), O(n)
3. O(1), O(log n)
4. O(1), O(log n)

답: 1
해설:

최선의 경우: 첫 번째 원소에서 찾음 → O(1)

최악의 경우: 마지막에 찾거나 없을 때 → O(n)

문제 3.

선형 검색과 이진 검색 연산 중에서 분할 정복 알고리즘의 기법으로 설계된 검색 연산은 (　　　　) 연산이다.

답: 이진 검색

3-3

문제 1.

다음은 알파벳 순으로 정렬된 배열이다.

{BAT, CAT, EAT, FAT, JAT, LAT}

여기에 DAT라는 원소를 추가할 때, 가장 먼저 그 위치를 바꾸는 원소는 무엇인가?

1. EAT
2. FAT
3. JAT
4. LAT

답: 4

문제 2.

다음은 알파벳 순으로 정렬된 배열이다.

{BAT, CAT, EAT, FAT, JAT, LAT}

여기에 EAT라는 원소를 제거할 때, 가장 먼저 그 위치를 바꾸는 원소는 무엇인가?

1. LAT
2. FAT
3. EAT
4. JAT

답: 2

문제 3.

n개의 원소를 가진 정렬된 배열에 대한 추가 연산과 삭제 연산의 시간 복잡도는 (　　　　)이다.
답: O(n)

4-1

문제 1.

배열에서는 원소의 위치와 접근 시간의 연관성이 없다. 이러한 성질을 (　　　　)라고 한다.
답: random access

문제 2.

연결 리스트는 데이터와 링크의 결합인 (　　　　)로 이루어져 있다.
답: 노드 (node)

문제 3.

연결 리스트의 각 노드는 다음 노드를 가리키는 (　　　　)을(를) 포함하고 있다.
답: 링크

4-2

문제 1.

각 노드가 하나의 노드와 연결된 연결 리스트를 (　　　　)(이)라고 한다.
답: 단일 연결 리스트

문제 2.

n개의 원소가 저장된 단일 연결 리스트의 제거 연산의 시간 복잡도를 다음 중에서 선택하시오.

1. O(n log n)
2. O(log n)
3. O(1)
4. O(n)

답: 4

4-3

문제 1.

각 노드가 두개의 노드와 연결된 연결 리스트를 (　　　　)(이)라고 한다.
답: 이중 연결 리스트

문제 2.

“n개의 원소가 저장된 이중 연결 리스트의 제거 연산의 시간 복잡도는 추가 연산의 시간 복잡도와 같다“라는 문장의 참과 거짓을 쓰시오. (참 또는 거짓을 쓸 것)
답: 참

해설:  삽입/삭제 모두 O(1) (단, 해당 노드를 알고 있는 경우)

문제 3.

 “n개의 원소가 저장된 이중 연결 리스트의 제거 연산의 시간 복잡도는 단일 연결 리스트의 제거 연산의 시간 복잡도보다 더 크다“라는 문장의 참과 거짓을 쓰시오. (참 또는 거짓을 쓸 것)
답: 거짓

해설:

단일 연결 리스트는 이전 노드를 찾기 위해 O(n)이 걸릴 수 있지만,

이중 연결 리스트는 이전 노드를 쉽게 알 수 있어 제거 시 더 효율적일 수 있다

자료구조의 소개

자료란 무엇인가?

• 시스템에서 제공하는 자료형
• 사용자가 정의하는 자료형

자료의 관리

1. 추가

2. 제거

3. 검색

검색을 가장 빈번하게 사용하므로 가장 중요

검색의 3가지 종류

1. 임의의 원소 찾기 (Find arbitrary)
2. 가장 먼저/늦게 온 원소 찾기 (Find earliest/last)
3. 최대/최소인 원소 찾기 (Find top)

효율적인 기법

1. 기법이란 무엇인가?

• 기법(테크닉)
• 자료를 적절한 구조 (structure)를 갖도록 조직하고 그에 따른 연산 (operation)을 제공
• 구조 (structure)
• 개별적인 자료들이 목적에 적합한 관계를 갖도록 배치된 상태

구조 1. 리스트 (list)

자료를 한곳에 보관하기

구조 2. 정렬된 리스트 (sorted list)

검색을 쉽게 정렬한 리스트

구조 3. 큐 (queue)

도착한 순서대로 정렬한 리스트

구조 4. 계층 구조 (hierarchy)

족보를 표현하는 법

구조 5. 그래프 (graph)

관계를 시각적으로 표현

추상화

공통된 속성을 추출하여 이를 이용하는 과정
추상 자료형: c++이나 Java의 클래스 개념으로 구현

2. 효율이란?

어떤 성과를 얻기 위해서 얼마나 많은 자원을 투입하였는지 측정
성능이라고도함
= solution/resource

1. 최선의 경우 -> 최고기록
2. 평균의 경우 -> 평점
3. 최악의 경우 -> 대기 시간

컴퓨터의 자원

1. 시간 = cpu
2. 공간 = memory

시간이 더 중요함 (비쌈)

자료구조의 성능

입력된 자료의 크기에 따른 시간의 증가 속도를 표현