자료구조 퀴즈 1~4주차

🍀 강의 수강 기록/자료구조

자료구조 퀴즈 1~4주차

수구마 2025. 4. 24. 00:44

2025. 4. 24. 00:44

1-1

문제 1.

우리가 사용하는 다양한 앱에서는 (　　　　)를 효율적으로 관리하는 기법이 구현되어 있다.
답: 자료

문제 2.

기차표 예매와 수강 신청 등을 관리하는 시스템에서는 자료와 함께 (　　　　)를 관리한다.
답: 순서

1-2

문제 1.

다음 문장의 빈칸에 들어갈 말은?

컴퓨터에 저장할 수 있도록 프로그래밍 언어에서 미리 정의된 값들의 집합을 (　　　　)이라고 한다.

답: 자료형

문제 2.

16 bit로 세상의 모든 문자를 표현할 수 있는 체계를 (　　　　)라고 한다.

EBCDIC 코드
Uni 코드
BCD 코드
ASCII 코드

답: 2. Unicode

해설:

ASCII: 7bit (128자만 표현 가능)
EBCDIC: IBM의 8bit 문자 인코딩
BCD: Binary-Coded Decimal, 숫자 표현 방식
Unicode: 다양한 언어의 문자를 16bit 이상으로 표현 가능한 체계

문제 3.

정수형 표현에서 1의 보수와 2의 보수는 (　　　　)을(를) 표현하기 위한 방법이다.
답: 음수

1-3

문제 1.

다음 문장의 참과 거짓을 판정하시오.

정렬된 리스트에서는 자료의 위치를 예측할 수 있기 때문에 효율적인 검색이 가능하다.

답: 참

문제 2.

자료를 만난 순서에 따라서 저장하는 구조를 다음 중에서 선택하시오.

큐
리스트
스택
배열

답: 1

문제 3.

족보와 같은 계층 구조를 효율적으로 표현하는 구조를 (　　　　)(이)라고 한다.
답: 트리

2-1

문제 1.

특정한 프로그램을 수행하는 데 요구되는 메모리의 크기를 (　　　　)(이)라고 한다.
답: 공간 복잡도

문제 2.

점근적 분석법에서 성능은 (　　　　)에 따라서 결정된다.
답: 입력의 크기

문제 3.

다음 네 가지 표현 중에서 그 의미가 다른 것은 무엇인가?

f(n)의 하한은 g(n)임
최악의 경우에도 f(n)은 g(n)보다 좋음
g(n)은 f(n)보다 성능이 나쁨
f(n) ≤ g(n)

답: 1

해설:

"하한"은 보통 Ω(𝑔(𝑛))를 의미 → f(n)이 최소한 g(n)만큼의 성능을 요구함 → 나머지 선택지들과 방향이 다름
~ 4. 모두 f(n)이 g(n)보다 작거나 같다는 식의 의미를 갖고 있어, 상대적으로 f(n)의 성능이 더 좋다는 쪽에 가까움

2-2

문제 1.

f(n) = O(5n log n)이라면, f(n) = O(g(n))이다에서 g(n)에 올 수 없는 함수는?

n log n
n
n³
n²

답: 2

문제 2.

If g(n) ≥ M f(n) for n > n₀, then g(n) = (　　　　). 에서 (　　　　)에 들어갈 식은?

답: Ω(f(n))

해설:
g(n) ≥ M·f(n) for n > n₀ 은 f(n)에 대한 하한(bound from below)을 의미

문제 3.

f(n) = O(n² + n)이라면, f(n) = O(g(n))이다. g(n)에 올 수 없는 함수는?

n³
n
n²
n⁴

답: 2

해설:
f(n) = O(n² + n) 은 O(n²)와 같다고 볼 수 있음
(n²), (n³), (n⁴) → f(n)의 상한이 될 수 있음
하지만 n은 f(n)보다 작기 때문에 상한으로는 올 수 없음

2-3

문제 1.

n 명인 반의 학생들이 모두 키 순으로 앉아있다. 여기에 새로운 학생 한 명이 전학을 왔다. 이 학생을 그냥 맨 앞에 앉도록 할 때, 걸리는 시간 복잡도는 무엇인가?

O(n)
O(n log n)
O(1)
O(log n)

답: 1

문제 2.

int func (int n) {
  for (k = 1; k < n; k = k * 10)
    printf("hello");
}

다음 함수의 시간 복잡도를 n의 함수로 나타내시오.

O(log n)
O(n log n)
O(n²)
O(n)

답: 1

문제 3.

다음 중 시간 복잡도가 가장 큰 함수는 무엇인가?

O(nⁿ)
O(n¹⁰⁰)
O(n!)
O(2ⁿ)

답: 1

해설:
(시간 복잡도 크기 순으로 정리):
𝑂(𝑛¹⁰⁰) → 다항식 (Polynomial)
𝑂(2ⁿ) → 지수 함수 (Exponential)
𝑂(𝑛!) → 팩토리얼 (Factorial)
𝑂(𝑛ⁿ) → 지수보다도 빠르게 커지는 초지수 함수

3-1

문제 1.

리스트의 가장 중요한 성질은 모든 원소들이 (　　　　)에 1:1로 대응된다는 점이다.
답: 인덱스

문제 2.

연결 리스트는 리스트를 (　　　　)에 기반하여 구현한 자료구조이다.
답: 포인터

문제 3.

“정렬되지 않은 리스트에서 원소를 추가하는 연산은 정렬된 리스트에서 원소를 추가하는 연산보다 더 좋은 시간 복잡도를 보인다”는 문장의 참과 거짓을 쓰시오.(참 또는 거짓을 쓸 것)
답: 참

3-2

문제 1.

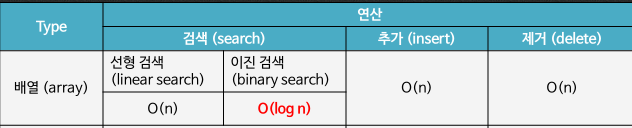
n개의 원소를 가진 배열에 대한 이진 검색의 시간 복잡도는 (　　　　)이다.

오답: O(n) -> 이건 선형검색

정답: O(log n)

해설:

매번 검색 범위를 절반으로 줄임

문제 2.

n개의 원소를 가진 배열에 대한 선형 검색은 최선의 경우에는 [ ]의 시간이 걸리지만 최악의 경우에는 [ ]의 시간이 걸린다. 빈칸을 Big-O 표기법으로 표현한 쌍 중에서 맞는 것은?

O(1), O(n)
O(log n), O(n)
O(1), O(log n)
O(1), O(log n)

답: 1
해설:

최선의 경우: 첫 번째 원소에서 찾음 → O(1)

최악의 경우: 마지막에 찾거나 없을 때 → O(n)

문제 3.

선형 검색과 이진 검색 연산 중에서 분할 정복 알고리즘의 기법으로 설계된 검색 연산은 (　　　　) 연산이다.

답: 이진 검색

3-3

문제 1.

다음은 알파벳 순으로 정렬된 배열이다.

{BAT, CAT, EAT, FAT, JAT, LAT}

여기에 DAT라는 원소를 추가할 때, 가장 먼저 그 위치를 바꾸는 원소는 무엇인가?

답: 4

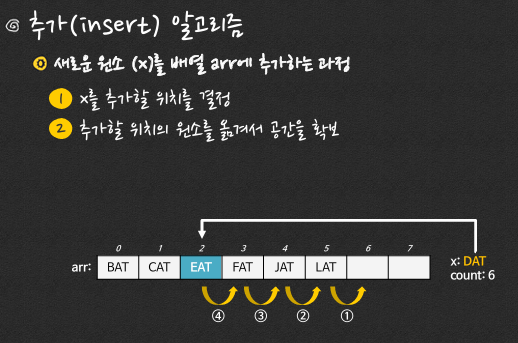
문제 2.

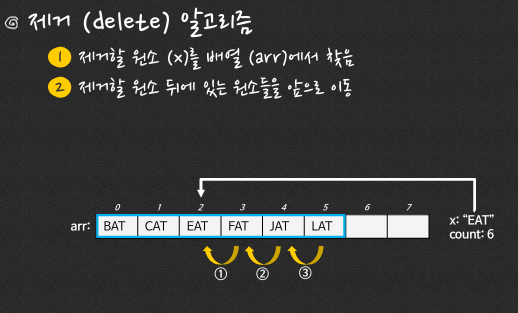
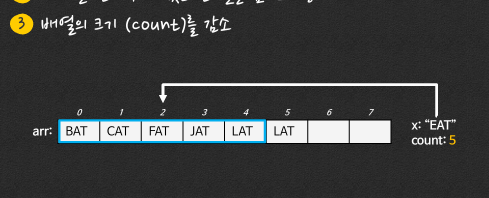
다음은 알파벳 순으로 정렬된 배열이다.

{BAT, CAT, EAT, FAT, JAT, LAT}

여기에 EAT라는 원소를 제거할 때, 가장 먼저 그 위치를 바꾸는 원소는 무엇인가?

답: 2

문제 3.

n개의 원소를 가진 정렬된 배열에 대한 추가 연산과 삭제 연산의 시간 복잡도는 (　　　　)이다.
답: O(n)

4-1

문제 1.

배열에서는 원소의 위치와 접근 시간의 연관성이 없다. 이러한 성질을 (　　　　)라고 한다.
답: random access

문제 2.

연결 리스트는 데이터와 링크의 결합인 (　　　　)로 이루어져 있다.
답: 노드 (node)

문제 3.

연결 리스트의 각 노드는 다음 노드를 가리키는 (　　　　)을(를) 포함하고 있다.
답: 링크

4-2

문제 1.

각 노드가 하나의 노드와 연결된 연결 리스트를 (　　　　)(이)라고 한다.
답: 단일 연결 리스트

문제 2.

n개의 원소가 저장된 단일 연결 리스트의 제거 연산의 시간 복잡도를 다음 중에서 선택하시오.

O(n log n)
O(log n)
O(1)
O(n)

답: 4

4-3

문제 1.

각 노드가 두개의 노드와 연결된 연결 리스트를 (　　　　)(이)라고 한다.
답: 이중 연결 리스트

문제 2.

“n개의 원소가 저장된 이중 연결 리스트의 제거 연산의 시간 복잡도는 추가 연산의 시간 복잡도와 같다“라는 문장의 참과 거짓을 쓰시오. (참 또는 거짓을 쓸 것)
답: 참

해설: 삽입/삭제 모두 O(1) (단, 해당 노드를 알고 있는 경우)

문제 3.

“n개의 원소가 저장된 이중 연결 리스트의 제거 연산의 시간 복잡도는 단일 연결 리스트의 제거 연산의 시간 복잡도보다 더 크다“라는 문장의 참과 거짓을 쓰시오. (참 또는 거짓을 쓸 것)
답: 거짓

해설:

단일 연결 리스트는 이전 노드를 찾기 위해 O(n)이 걸릴 수 있지만,

이중 연결 리스트는 이전 노드를 쉽게 알 수 있어 제거 시 더 효율적일 수 있다

'🍀 강의 수강 기록 > 자료구조' 카테고리의 다른 글

자료구조 2주차 성능 분석 (0)	2025.04.24
자료구조 1주차 자료구조의 소개 (1)	2025.04.22

개발로그

🍀 강의 수강 기록/자료구조